Chapter 5B

(AST405) Lifetime data analysis

Author

Md Rasel Biswas

5 Inference Procedures for Log-location-scale Distributions

5.1 Log-normal and normal distributions

Log-normal distribution

  • \(T\) follows a log-normal distribution with location parameter \(\mu\) and scale parameter \(\sigma\) if \(Y=\log T\sim\mathcal{N}(\mu, \sigma^2)\)

  • The pdf and survivor function of log-normal distribution \[\begin{aligned} f(t; \mu, \sigma) &= \frac{1}{\sigma t \sqrt{2\pi}}\exp\bigg[-\frac{1}{2}\bigg(\frac{\log t -\mu}{\sigma}\bigg)^2\bigg]\\[.35em] S(t; \mu, \sigma) & = 1 - \Phi\bigg(\frac{\log t -\mu}{\sigma}\bigg) \end{aligned}\]

    • \(\mu\) and \(\sigma\) are the parameters of both normal and log-normal distributions

    • \(\Phi(\cdot)\,\rightarrow\) cumulative distribution function of standard normal distribution

  • Log-normal distribution is a member of the log-location-scale family of distributions and the corresponding location-scale distribution is normal with \[\begin{aligned} S_0(z) & = 1 - \Phi(z) \\ f_0(z) & = \frac{1}{\sqrt{2\pi}}e^{-z^2/2}=\phi(z) \end{aligned}\]

    • \(\phi(\cdot)\,\rightarrow\) pdf of standard normal distribution

    • \(z=(y-\mu)/\sigma\)

  • Density function of log-lifetime \[\begin{aligned} f(y; \mu, \sigma) &= \frac{1}{\sigma}f_0\Big(\frac{y-\mu}{\sigma}\Big) \\ &=\frac{1}{\sigma\sqrt{2\pi}}\exp\Big[-\frac{1}{2}\Big(\frac{y-\mu}{\sigma}\Big)^2\Big] \end{aligned}\]

  • Survivor function of log-lifetime \[\begin{aligned} S(y; \mu, \sigma) = S_0\bigg(\frac{y-\mu}{\sigma}\bigg) = 1 - \Phi\bigg(\frac{y-\mu}{\sigma}\bigg) \end{aligned}\]

Likelihood function normal distribution

  • Data \[ \big\{(t_i, \delta_i), \;i=1, \ldots, n\big\} \]

  • Log-likelihood function \[\begin{aligned} \ell(\mu, \sigma) & = \log \prod_{i=1}^n\Big[({1}/{\sigma})\,f_0(z_i)\Big]^{\delta_i}\,\Big[S_0(z_i)\Big]^{1-\delta_i}\\ &=-r\log \sigma + \sum_{i=1}^n \delta_i\log f_0(z_i) + \sum_{i=1}^n(1-\delta_i)\log S_0(z_i) \\ &= -r\log \sigma -\frac{1}{2}\sum_{i=1}^n \delta_iz_i^2 + \sum_{i=1}^n(1-\delta_i)\log S_0(z_i) \end{aligned}\]

    • \(z_i=(y_i - \mu)/\sigma\) and \(y_i=\log t_i\)

    • \(r = \sum_{i=1}^n \delta_i\)

  • Elements of hessian matrix and score function depend on the followings \[\begin{aligned} \frac{\partial \log f_0(z)}{\partial z} &= -z \\ \frac{\partial^2 \log f_0(z)}{\partial z^2} &= -1 \\ \frac{\partial \log S_0(z)}{\partial z} &= -\frac{f_0(z)}{S_0(z)} \\ \frac{\partial^2 \log S_0(z)}{\partial z^2} &= \frac{zf_0(z)}{S_0(z)} - \bigg[\frac{f_0(z)}{S_0(z)}\bigg]^2 \end{aligned}\]

  • MLEs \[\begin{aligned} (\hat\mu, \hat\sigma)' = {\arg\,\max}_{\Theta} \;\ell(\mu, \sigma) \end{aligned}\]

    • Sampling distribution \[\begin{aligned} (\hat\mu, \hat\sigma)' \sim \mathcal{N}\Big((\mu, \sigma)', V\Big) \end{aligned}\] where \[ \hat V = \Big[-H(\hat \mu, \hat \sigma)\Big]^{-1} \]

  • Confidence intervals of parameters, quantiles, and survival probabilities can be obtained using the methods described for Weibull models

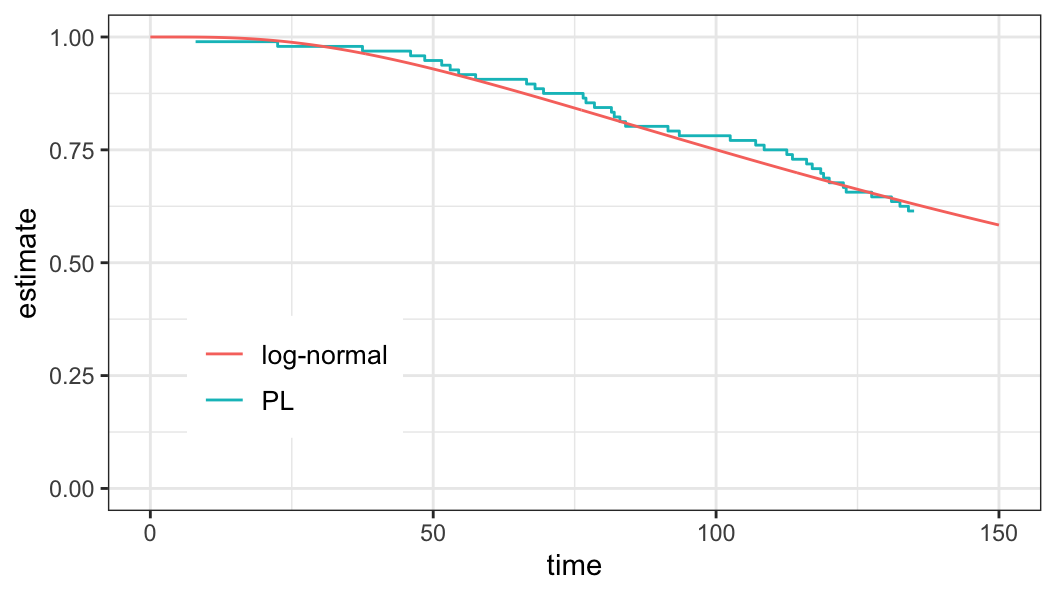
  • Estimate of survivor function (Log-normal distribution) \[\begin{aligned} S(t; \hat\mu, \hat\sigma) &= 1 - \Phi\Big(\frac{\log t - \hat\mu}{\hat\sigma}\Big)\notag\\ &=1 - \Phi(\hat\psi) \end{aligned}\] where \[ \hat\psi = \Phi^{-1} \Big(1-S(t; \hat\mu, \hat\sigma)\Big)= \frac{\log t - \hat\mu}{\hat\sigma} \]

    • Standard error of \(\hat\psi\) \[ se(\hat\psi) = \sqrt{\mathbf{a}'\hat V\mathbf{a}} \] where \[ \mathbf{a} = (-1/\hat\sigma, -\hat\psi/\hat\sigma)' \]

Estimate of survivor function

  • \((1-\alpha)100\%\) CI of \(S(t)\) \[\begin{aligned} L&<\psi < U\\ L &<\Phi^{-1}\big(1 - S(t;\mu, \sigma)\big) < U\\ \Phi(L) &<1 - S(t;\mu, \sigma)<\Phi(U)\\ 1-\Phi(U) &<S(t;\mu, \sigma)<1-\Phi(L) \end{aligned}\] where \[\begin{aligned} L & = \hat\psi -z_{1-\alpha/2}\,se(\hat\psi) \\ U & = \hat\psi +z_{1-\alpha/2}\,se(\hat\psi) \end{aligned}\]

  • LRT statistics based method of obtaining CI for survivor function is described with \[H_0: S(y_0) = S(\log t_0)=s_0\]

  • The \(100(1-\alpha)\%\) CI for \(S(t)\) can be obtained from the values of \(s_0\) that satisfy \[ \Lambda(s_0)=2\ell(\hat\mu, \hat\sigma) - 2\ell(\tilde \mu, \tilde \sigma)\leq \chi^2_{(1), 1-\alpha} \]

  • Unrestricted and unrestricted MLEs are obtained as \[\begin{aligned} \text{unrestricted}\;\;\;(\hat\mu, \hat\sigma)'&={\arg\,\max}_{\Theta}\,\ell(\mu, \sigma) \\ \text{restricted}\;\;\;(\tilde\mu, \tilde\sigma)'&={\arg\,\max}_{\Theta}\,\ell(y_0-\sigma\Phi^{-1}(1-s_0), \sigma) \end{aligned}\] where under \(H_0\), we can show \[ S(y_0) = 1 - \Phi\Big(\frac{y_0 - \mu}{\sigma}\Big) = s_0\;\;\Rightarrow\;\;\mu = y_0 - \sigma\Phi^{-1}(1-s_0) \]

Quantiles

  • The expression of estimate of \(y_p\) \[ \hat y_p = \hat\mu + \hat \sigma w_p \] where for normal distribution \[ w_p = S_0^{-1}(1-p) = \Phi^{-1}(p) \]
  • Standard error of \(\hat y_p\)
    \[ se(\hat y_p) = \sqrt{\mathbf{a}'\hat V\mathbf{a}} \] where \[ \mathbf{a} = (1, w_p)' \]

Homework

  • Obtain the expressions of Wald-type and LRT based \(100(1-\alpha)\%\) confidence intervals of \(y_p\)

Example 5.3.1

  • Data are available on lifetimes (in thousand miles) of 96 locomotive controls, of which were failed.

  • The test was terminated after \(135K\) miles, so 59 lifetimes were censored at \(135K\).

dat_ex531
# A tibble: 96 × 2
    time status
   <dbl>  <int>
 1  22.5      1
 2  37.5      1
 3  46        1
 4  48.5      1
 5  51.5      1
 6  53        1
 7  54.5      1
 8  57.5      1
 9  66.5      1
10  68        1
# ℹ 86 more rows
dat_ex531 %>% 
  count(status)
# A tibble: 2 × 2
  status     n
   <int> <int>
1      0    59
2      1    37

Log-normal and normal model fit

mod_LN <- survreg(Surv(time, status) ~ 1, 
                  dist = "lognormal",
                  data = dat_ex531)
mod_N <- survreg(Surv(log(time), status) ~ 1, 
                dist = "gaussian",
                data = dat_ex531)

MLEs \((\hat\mu, \log\hat\sigma)\) and corresponding standard errors

tidy(mod_LN)
# A tibble: 2 × 5
  term        estimate std.error statistic p.value
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    5.19      0.129     40.3    0    
2 Log(scale)    -0.136     0.131     -1.04   0.297

Estimated variance of \((\hat\mu, \log\hat\sigma)\)

mod_LN$var
            (Intercept) Log(scale)
(Intercept)  0.01657557 0.00983969
Log(scale)   0.00983969 0.01703353

Estimated variance \(\operatorname{V}(\hat\mu, \hat\sigma)\) from \(\operatorname{V}(\hat\mu, \log\hat\sigma)\)

  • \(G\,V(\hat\mu, \log\hat\sigma)\,G'\)
           [,1]       [,2]
[1,] 0.01657557 0.00858735
[2,] 0.00858735 0.01297359

\[G = \begin{bmatrix} 1 & 0 \\ 0 & \exp(\sigma)\end{bmatrix}\]

95% Confidence intervals for \(\mu\) and \(\sigma\)
par lower upper lower upper
\(\mu\) 4.942 5.447 5.000 5.400
\(\sigma\) 0.676 1.127 0.709 1.109

  • Estimate of \(S(80)\) \[\begin{aligned} S(80; \hat\mu, \hat\sigma) &= 1 - \Phi\Big(\frac{\log 80 - \hat\mu}{\hat\sigma}\Big)\\ &=0.824 \end{aligned}\]

    • \(\hat\mu = 5.195 \;\;\text{and}\;\; \hat\sigma = 0.873\)

Comparison of the estimates of survivor function

`

Estimate and confidence interval of \(S(80)\)
parameter est lower upper
\(S(80)\) 0.824 0.667 0.924
  • Obtain LRT based 95% CI for \(S(80)\)

Quantiles

  • General expression of \(p\)th quantile of log-lifetime (\(\hat\mu=5.195\) and \(\hat \sigma = 0.873\)) \[ \hat y_p = \hat\mu + \hat\sigma w_p \]
    • \(w_p=\Phi^{-1}(p)\)
Estimate and confidence intervals of different quantiles of locomotive controls lifetime (normal distribution)
\(p\) \(w_p\) \(\hat y_p\) se lower upper
0.25 -0.674 4.606 0.105 NA NA
0.50 0.000 5.195 0.129 NA NA
0.75 0.674 5.783 0.194 NA NA

5.2 Log-logistic and logistic distributions

Log-logistic distribution

  • \(T\) follows a log-logistic distribution with parameters \(\alpha\) (scale) and \(\beta\) (shape) if \(Y=\log T\) follows a logistic distribution with parameters \(u\) (location) and \(b\) (scale)
  • The pdf, survivor, and hazard function of log-logistic distribution \[\begin{aligned} f(t; \alpha, \beta) &= \frac{(\beta/\alpha)(t/\alpha)^{\beta-1}}{\big[1+(t/\alpha)^{\beta}\big]^2}\\[.45em] S(t; \alpha, \beta) & =\big[1 + (t/\alpha)^{\beta}\big]^{-1} \\[.45em] h(t; \alpha, \beta) &= \frac{(\beta/\alpha)(t/\alpha)^{\beta-1}}{\big[1+(t/\alpha)^{\beta}\big]} \end{aligned}\]

Logistic distribution

  • Log-logistic distribution is a member of the log-location-scale family of distributions and the corresponding location-scale distribution is logistic with \[\begin{aligned} S_0(z) & =\frac{1}{1 + e^z} \\[.25em] f_0(z) & =\frac{e^z}{(1 + e^z)^2} \end{aligned}\]

    • \(z=(y-u)/b\)

  • Density function of log-lifetime \[\begin{aligned} f(y; u, b) &= \frac{1}{b}f_0\Big(\frac{y-u}{b}\Big) \\[.3em] &=\frac{(1/b)\,\exp\big[{(y-u)/b}\big]}{\big\{1 + \exp\big[(y-u)/b\big]\big\}^2} \end{aligned}\]

  • Survivor function of log-lifetime \[\begin{aligned} S(y; u, b) &= S_0\bigg(\frac{y-u}{b}\bigg) \\ & = \frac{1}{1 + \exp\big[(y-u)/b\big]} \end{aligned}\]

  • Data: \(\;\;\;\big\{(t_i, \delta_i), \;i=1, \ldots, n\big\}\)

  • Log-likelihood function \[\begin{aligned} \ell(\mu, \sigma) & = \log \prod_{i=1}^n\Big[({1}/{b})\,f_0(z_i)\Big]^{\delta_i}\,\Big[S_0(z_i)\Big]^{1-\delta_i}\notag\\ &=-r\log b + \sum_{i=1}^n \delta_i\log f_0(z_i) + \sum_{i=1}^n(1-\delta_i)\log S_0(z_i)\notag\\ &=-r\log b + \sum_{i=1}^n\Big[\delta_i\big\{z_i - \log(1+e^{z_i})\big\} - \log(1+e^{z_i})\Big]\notag %& = -r\log b + \sum_{i=1}^n\Big[\delta_i z_i + (1 - \delta_i)\log(1+e^{z_i})\Big] \end{aligned}\]

    • \(z_i=(y_i - u)/b\) and \(y_i=\log t_i\)

    • \(r = \sum_{i=1}^n \delta_i\)

  • Elements of hessian matrix and score function depend on the followings \[\begin{aligned} \frac{\partial \log f_0(z)}{\partial z} &= 1 - \frac{2e^z}{1+e^z} \\ \frac{\partial^2 \log f_0(z)}{\partial z^2} &= -2f_0(z) \\ \frac{\partial \log S_0(z)}{\partial z} &= \frac{-e^z}{1+e^z} \\ \frac{\partial^2 \log S_0(z)}{\partial z^2} &= \frac{-e^z}{(1+e^z)^2} \end{aligned}\]

  • MLEs \[\begin{aligned} (\hat u, \hat b)' = {\arg\,\max}_{\Theta} \;\ell(u, b) \end{aligned}\]

  • Sampling distribution \[\begin{aligned} (\hat u, \hat b)' \sim \mathcal{N}\Big((u, b)', V\Big) \end{aligned}\] where \[ \hat V = \Big[-H(\hat u, \hat b)\Big]^{-1} \]

  • Confidence intervals of parameters, quantiles, and survival probabilities can be obtained using the methods described for Weibull models

  • Estimate of survivor function (logistic distribution) \[\begin{aligned} S_0\Big(\frac{y-\hat u}{\hat b}\Big)=S(y; \hat u, \hat b) &= \frac{1}{1+\exp\big[(y -\hat u)/\hat b\big]} \\[.5em] \log\bigg[\frac{1-S(y)}{S(y)}\bigg] & = \frac{y-\hat u}{\hat b} = {\color{purple}\hat\psi} = S_0^{-1}\Big(S(y)\Big) \end{aligned}\]

    • Standard error of \(\hat\psi\) \[ se(\hat\psi) = \sqrt{\mathbf{a}'\hat V\mathbf{a}},\;\;\;\text{where } \mathbf{a} = (-1/\hat b, -\hat\psi/\hat b)' \]

\((1-\alpha)100\%\) CI of \(S(t)\)

\[\begin{aligned} L&<\psi < U\\ L &< \log \frac{1-S(y)}{S(y)} < U\\ \exp(L) &< \frac{1-S(y)}{S(y)} <\exp(U)\\ 1 + \exp(L) &< 1 + \frac{1-S(y)}{S(y)} <1 + \exp(L) \\ \frac{1}{1 + \exp(U)} &<S(y) < \frac{1}{1 + \exp(L)} \end{aligned}\] where \[\begin{aligned} L & = \hat\psi -z_{1-\alpha/2}\,se(\hat\psi) \\ U & = \hat\psi +z_{1-\alpha/2}\,se(\hat\psi) \end{aligned}\]

Estimate of survivor function

  • LRT statistics based method of obtaining CI for survivor function is described with \[H_0: S(y_0) = S(\log t_0)=s_0\]

  • The \(100(1-\alpha)\%\) CI for \(S(t)\) can be obtained from the values of \(s_0\) that satisfy \[ \Lambda(s_0)\leq \chi^2_{(1), 1-\alpha} \] where \[\begin{aligned} \Lambda(s_0) = 2\ell(\hat u, \hat b) - 2\ell(\tilde u, \tilde b) \end{aligned}\]

  • Unrestricted and unrestricted MLEs are obtained as \[\begin{aligned} \text{unrestricted}\;\;\;(\hat u, \hat b)'&={\arg\,\max}_{\Theta}\,\ell(u, b) \\ \text{restricted}\;\;\;(\tilde u, \tilde b)'&={\arg\,\max}_{\Theta}\,\ell\big(y_0-b\log\big\{(1-s_0)/s_0\big\}, b\big) \end{aligned}\] where under \(H_0\), we can show \[ S(y_0) = s_0\;\;\Rightarrow\;\;u = y_0 - b\log\frac{1-s_0}{s_0} \]

Quantiles

  • The expression of estimate of \(y_p\) \[ \hat y_p = \hat u + \hat b w_p \] where for normal distribution \[ w_p = S_0^{-1}(1-p) = \log\frac{p}{1-p} \]
  • Standard error of \(\hat y_p\)
    \[ se(\hat y_p) = \sqrt{\mathbf{a}'\hat V\mathbf{a}} \] where \[ \mathbf{a} = (1, w_p)' \]

Homework

  • Obtain the expressions of Wald-type and LRT based \(100(1-\alpha)\%\) confidence intervals of \(y_p\)

Example 5.3.1

  • Data are available on lifetimes (in thousand miles) of 96 locomotive controls, of which were failed.

  • The test was terminated after \(135K\) miles, so 59 lifetimes were censored at \(135K\).

dat_ex531
# A tibble: 96 × 2
    time status
   <dbl>  <int>
 1  22.5      1
 2  37.5      1
 3  46        1
 4  48.5      1
 5  51.5      1
 6  53        1
 7  54.5      1
 8  57.5      1
 9  66.5      1
10  68        1
# ℹ 86 more rows
dat_ex531 %>% 
  count(status)
# A tibble: 2 × 2
  status     n
   <int> <int>
1      0    59
2      1    37

Log-logistic and logistic model fit

mod_LL <- survreg(Surv(time, status) ~ 1, 
                  dist = "loglogistic",
                  data = dat_ex531)
mod_L <- survreg(Surv(log(time), status) ~ 1, 
                dist = "logistic",
                data = dat_ex531)

MLEs \((\hat u, \log\hat b)\)

[1]  5.1206418 -0.8266704

Estimated variance of \((\hat u, \log\hat b)\)

            (Intercept)  Log(scale)
(Intercept) 0.010490062 0.007837215
Log(scale)  0.007837215 0.022515937

MLEs of \((\hat u, \hat b)\)

[1] 5.1206418 0.4375036

Estimated variance of \((\hat u, \hat b)\)

            [,1]        [,2]
[1,] 0.010490062 0.003428809
[2,] 0.003428809 0.004309761
95% Confidence intervals for location and scale parameters
dist par est lower upper lower upper
Logistic \(u\) 5.121 4.920 5.321 5.000 5.300
NA \(b\) 0.438 0.326 0.587 0.360 0.559
Gaussian \(\mu\) 5.195 4.942 5.447 5.000 5.400
NA \(\sigma\) 0.873 0.676 1.127 0.709 1.109

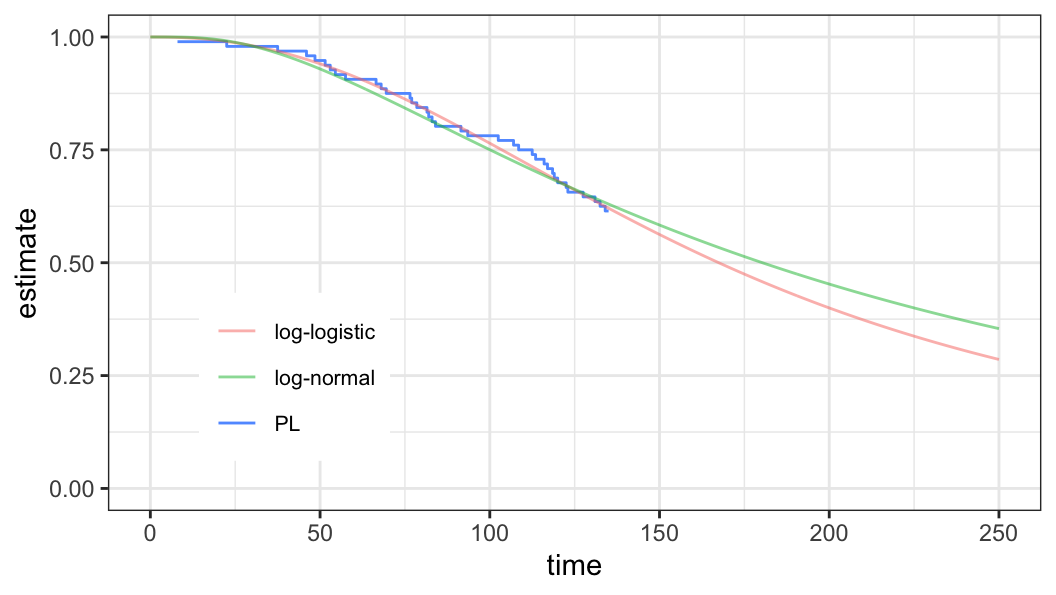
  • Estimate of \(S(80)\) (log-logistic distribution) \[\begin{aligned} S(80; \hat u, \hat b) &= \frac{1}{1 + \exp\big[(\log 80 - \hat u)/{\hat b}\big]}\\ &=0.844 \end{aligned}\]

    • \(\hat u = 5.121 \;\;\text{and}\;\; \hat b = 0.438\)

Comparison of the estimates of survivor function

`

Estimate and corresponding Wald-type confidence interval of the survival probability \(S(80)\)
dist est lower upper
Log-logistic 0.844 0.566 0.957
Log-normal 0.824 0.667 0.924
  • Obtain LRT based 95% CI for \(S(80)\)

Quantiles

  • General expression of \(p\)th quantile of log-lifetime (\(\hat u=5.121\) and \(\hat b = 0.438\)) \[ \hat y_p = \hat u + \hat b w_p \]
    • \(w_p = \log\frac{p}{1-p}\)
Estimate and confidence intervals of different quantiles
dist \(p\) \(w_p\) \(\hat y_p\) se lower upper
Logistic 0.25 -1.099 4.640 0.143 NA NA
NA 0.50 0.000 5.121 0.102 NA NA
NA 0.75 1.099 5.601 0.234 NA NA
Gaussian 0.25 -0.674 4.826 0.101 NA NA
NA 0.50 0.000 5.121 0.102 NA NA
NA 0.75 0.674 5.416 0.177 NA NA

Homework

  • Analyze the locomotive control lifetimes using Weibull model and compare the results

5.3 Comparison of distributions

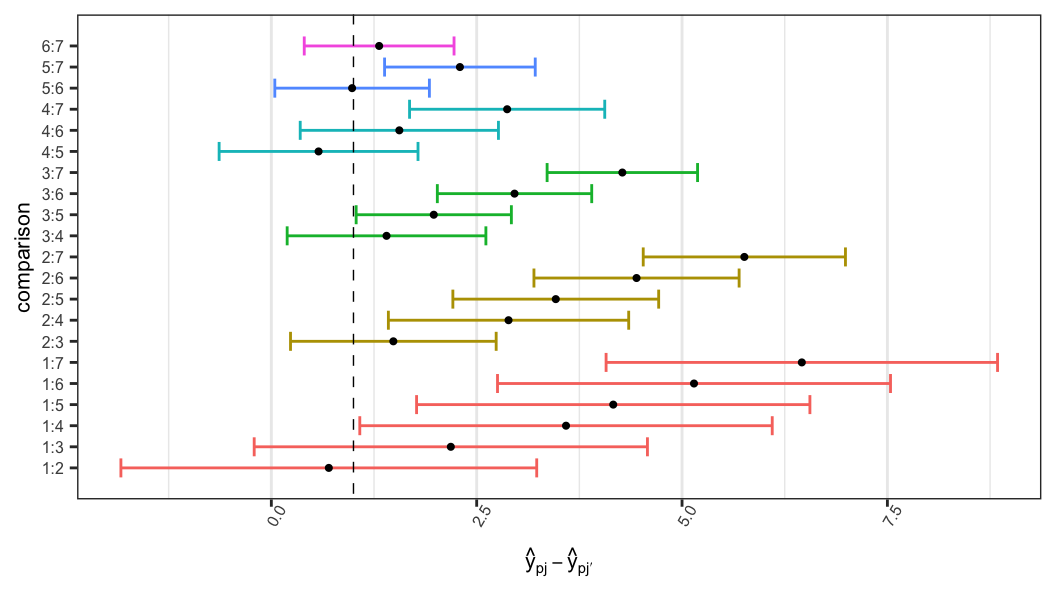
  • Let \(T_{ji}\) be the lifetime of \(i\)th subject of the \(j\)th group (\(i=1, \ldots, n_j\), \(j=1, \ldots, m\))

  • Assume \(T_{ji}\) follows a distribution of log-location-scale family with parameters \(\alpha_j\) (scale) and \(\beta_j\) (shape)

  • The corresponding distribution of log-lifetime \(Y_{ji}=\log T_{ji}\) is of a location-scale family distribution with parameters \(u_j\) (location) and \(b_j\) (scale) \[u_j = \log\alpha_j \;\; \text{and} \;\;b_j = (1/\beta_j)\]

Survivor functions

  • The survivor function of \(Y_{ji}=\log T_{ji}\) \[\begin{aligned} S_j(y) = S_0\Big(\frac{y-u_j}{b_j}\Big) \end{aligned}\]

  • The survivor function of \(T_{ji}\) \[\begin{aligned} S_j(t) = S_0^\star\big[(t/\alpha_j)^{\beta_j}\big] \end{aligned}\]

    • \(S_0^\star(x) = S_0(\log x)\)

    • \(u_j = \log \alpha_j\)

    • \(b_j = (1/\beta_j)\)

  • Comparison of several normal populations is a well-known problem in statistics, where equal population variances are assumed, and the comparisons are performed on the basis of equality of population means

Quantile

  • General expression of the \(p\)th quantile of the \(j\)th population takes the form \[\begin{aligned} y_{jp} = u_j + b_j w_p, \;\;\;j=1, \ldots, m \end{aligned}\]
    • \(w_p=S_0^{-1}(1-p)\)

Equality of two populations

  • When the scales are not equal (i.e. \(b_1\neq b_2\)), the difference between the \(p\)th quantiles does depend on the probability \(p\) \[\begin{aligned} y_{1p} - y_{2p} = u_1 - u_2 + w_p(b_1 - b_2) \end{aligned}\]

  • Under the assumption of equality of the scales (i.e. \(b_1 = b_2\)), difference between \(p\)th (log-lifetime) quantile of a pair of populations (say 1 and 2) is constant, i.e. it does not depend on the probability \(p\in (0, 1)\) \[ \begin{aligned} y_{1p} - y_{2p} = u_1 - u_2 \end{aligned} \]

  • The difference between two log-lifetime quantiles can be expressed in terms of the ratio of lifetime quantiles \[ \begin{aligned} y_{1p} - y_{2p} &= u_1 - u_2 \\[,25em] \log t_{1p} - \log t_{2p} &= \log \alpha_1 - \log \alpha_2 \\[.25em] t_{1p}/t_{2p} & = \alpha_1/\alpha_2 \end{aligned} \]

  • The ratio of the \(p\)th quantiles of two lifetime distributions does not depend on the probability \(p\) when the corresponding shape parameters are equal \((\beta_1=\beta_2)\)

  • Equality of all quantiles of two distributions, i.e. \[y_{1p}=y_{2p}\;\;\forall\;p\in(0, 1),\] corresponds to equality of two distributions, i.e. \[S_1(y)=S_2(y)\]

  • Under the assumption of common scale (shape for lifetime) parameter, the null hypothesis of equality of two distributions can be expressed as \[\begin{aligned} H_0: u_1-u_2=0\;\;\;\text{or}\;\;\;H_0:(\alpha_1/\alpha_2)=1 \end{aligned}\]

  • Equality of two populations with survivor functions (say \(S_1\) and \(S_2\)) can be expressed in terms of survivor functions

  • Since \[y_{1p}= y_{2p} + u_1 - u_2 \;\;\text{or}\;\; t_{1p}=t_{2p}(\alpha_1/\alpha_2),\] the corresponding survivor functions can be expressed as \[\begin{aligned} S_1(y + u_1 -u_2) = S_2(y)\\[.25em] S_1\big(t(\alpha_1/\alpha_2)\big) = S_2(t) \end{aligned}\]

  • That is, the survivor functions for \(Y\) are translations of one another by an amount \((u_1 - u_2)\) along the \(y\)-axis

Wald-type statistic

  • Data \(\;\;\;\big\{(t_{ji}, \delta_{ji}), i=1, 2\big\}\) and \(y_{ji}=\log t_{ji}\)

  • Two populations can be compared in terms of \(p\)th quantile \[ H_0: y_{1p} = y_{2p} \]

  • Corresponding pivotal quantity \[ Z_p = \frac{(\hat y_{1p}-\hat y_{2p})-(y_{1p}-y_{2p})}{\big[\operatorname{var}(\hat y_{1p}) + \operatorname{var}(y_{2p})\big]^{1/2}}\sim \mathcal{N}(0, 1)\;\;\text{under $H_0$} \]

    • The statistic \(Z_p\) can be used to obtain confidence interval for \((y_{1p}-y_{2p})\)

  • To test \(H_0: b_1=b_2\), the following pivotal quantity can be considered \[ Z_b = \frac{(\log \hat b_1 - \log \hat b_2) - (\log b_1 - \log b_2)}{[\operatorname{var}(\log \hat b_1) + \operatorname{var}(\log \hat b_2)]^{1/2}}\sim \mathcal{N}(0, 1)\;\;\text{under $H_0$} \]

    • The statistic \(Z_b\) can be used to obtain confidence interval for \((b_1/b_2)\)

  • When scales are equal, two populations can be compared with respect their location parameter \(H_0: u_1 = u_2\)

  • The corresponding pivotal quantity \[ Z_u = \frac{( \hat u_1 - \hat u_2) - ( u_1 - u_2)}{[\operatorname{var}(\hat u_1) + \operatorname{var}(\hat u_2)]^{1/2}}\sim \mathcal{N}(0, 1)\;\;\text{under $H_0$} \]

    • The statistic \(Z_u\) can be used to obtain confidence interval for \((u_1 - u_2)\)
  • Wald statistic cannot be used to test \[ H_0: u_1=u_2, b_1=b_2 \]

LRT based inference

  • Data \(\;\;\big\{(t_{ji}, \delta_{ji}), j=1, \ldots, m, i=1, \ldots, n_j\big\}\) and \(y_{ji}=\log t_{ji}\)

  • Different tests and confidence intervals of interest

    1. \(H_0: b_1=\cdots=b_m\)

    2. Confidence interval for \((b_1/b_2)\)

    3. Equality of several location parameters when scale parameters are equal \[\begin{aligned} H_0&: u_1=\cdots=u_m, b_1=\cdots=b_m \\ H_1&: \text{all $u_j$'s are not equal}, b_1=\cdots=b_m \end{aligned}\]

    4. Confident interval for \((u_1-u_2)\) when \(b_1=b_2\)

    5. Confidence interval for \((y_{1p}-y_{2p})\) when \(b_1\neq b_2\)

Case 1

  • Hypothesis of interest \[ H_0: b_1=\cdots = b_m = b \;\;(\text{say}) \tag{5.1}\]

  • Log-likelihood function \[\begin{aligned} \ell(u_1, \ldots, u_m, b_1, \ldots, b_m) & = \sum_{j=1}^m\ell_j(u_j, b_j) \end{aligned}\]

  • Contribution to log-likelihood function for the \(j\)th population \[\begin{aligned} \ell_j(u_j, b_j) = -r_j\log b_j + \sum_{i=1}^{n_j}\Big[\delta_i\log f_0(z_{ji}) + (1 - \delta_{ji})\log S_0(z_{ji})\Big]\notag \end{aligned}\]

    • \(r_j = \sum_i \delta_{ji}\)

  • LRT statistic \[\begin{aligned} \Lambda & =2\ell(\hat u_1, \ldots, \hat u_m, \hat b_1, \ldots, \hat b_m) -2\ell(\tilde u_1, \ldots, \tilde u_m, \tilde b, \ldots, \tilde b) \end{aligned}\]

    • \(\Lambda\sim \chi^2_{(m-1)}\) under the null hypothesis defined in Equation 5.1

  • MLEs

    • \((\hat u_j, \hat b_j)' = {\arg\,\max}_{\Theta} \;\ell_j(u_j, b_j),\;\;j=1, \ldots, m\)

    • \((\tilde u_1, \ldots, \tilde u_m, \tilde b, \ldots, \tilde b)' = {\arg\,\max}_{\Theta}\,\ell( u_1, \ldots, u_m, b, \ldots, b)\)

Case 2

  • To obtain confidence interval of \((b_1/b_2)\), consider \[H_0: (b_1/b_2) = a \;\;\Rightarrow\;\;H_0: b_1 =ab_2\]

  • \(100(1-\alpha)\%\) confidence interval of \((b_1/b_2)\) can be obtained from the range of \(a\) values that satisfy \[\Lambda(a)\leq \chi^2_{(1), 1-\alpha},\] where the LRT statistic \[\Lambda(a) = 2\ell(\hat u_1, \hat u_2, \hat b_1, \hat b_2)- 2\ell(\tilde u_1, \tilde u_2, a\tilde b_2,\tilde b_2)\]

    • \((\hat u_j, \hat b_j)' = {\arg\,\max}_{\Theta} \;\ell_j(u_j, b_j),\;\;j=1, 2\)

    • \((\tilde u_1, \tilde u_2, \tilde b_2)' = {\arg\,\max}_{\Theta}\,\ell( u_1, u_2, ab_2, b_2)\)

Case 3

  • Test equality of several location parameters when scale parameters are equal \[\begin{aligned} H_0 &: u_1= \cdots = u_m, \;b_1 = \cdots = b_m \\[.25em] H_1&: \text{all $u_j$'s are not equal}, \;b_1=\cdots = b_m \end{aligned}\]

  • MLEs

    • under \(H_0,\;\;\) \((u^\star, b^\star) = {\arg\,\max}_{\Theta}\,\ell(u, \ldots, u, b, \ldots, b)\)

    • under \(H_1,\;\;\) \((\tilde u_1, \ldots, \tilde u_m, \tilde b) = {\arg\,\max}_{\Theta}\,\ell(u_1, \ldots, u_m, b, \ldots, b)\)

  • LRT statistic \[ \Lambda = 2\ell(\tilde u_1, \ldots, \tilde u_m, \tilde b, \ldots, \tilde b) - 2\ell(u^\star, \ldots, u^\star, b^\star, \ldots, b^\star) \]

    • Under the null hypothesis, \(\Lambda\) follows \(\chi^2_{(m-1)}\) distribution

Case 4

  • To obtain a confidence interval of \((u_1 - u_2)\) when \(b_1=b_2\), consider the null and alternative hypothesis \[\begin{aligned} H_0: u_1-u_2=\delta, \;b_1=b_2\;\;\;\text{vs}\;\;\;H_1: u_1-u_2\neq \delta, \;b_1=b_2 \end{aligned}\]

  • LRT statistic \[ \Lambda(\delta) = 2\ell(\tilde u_1, \tilde u_2, \tilde b, \tilde b) - 2\ell(u_2^\star + \delta, u_2^\star, b^\star, b^\star) \]

    • under \(H_0,\;\;\) \((u^\star, b^\star) = {\arg\,\max}_{\Theta}\,\ell(u, u, b, b)\)

    • under \(H_1,\;\;\) \((\tilde u_1, \tilde u_2, \tilde b) = {\arg\,\max}_{\Theta}\,\ell(u_1, u_2, b, b)\)

  • \(100(1-\alpha)%\) confidence interval for \((u_1-u_2)\) can be obtained from the set of \(\delta\) values that satisfy \(\Lambda(\delta) \leq \chi^2_{(1), 1-\alpha}\)

Case 5

  • When \(b_1\neq b_2\), to obtain confidence interval for \((y_{1p} - y_{2p})\) consider the following hypothesis \[ H_0: y_{1p} - y_{2p} = \Delta\;\;\Rightarrow\;\;H_0: u_1 - u_2 = \Delta + (b_2 -b_1)w_p \]
    • \(w_p = S_0^{-1}(1-p)\)
  • LRT statistic \[ \Lambda(\Delta) = 2\ell(\hat u_1, \hat u_2, \hat b_1, \hat b_2) - 2\ell(\tilde u_1, \tilde u_2, \tilde b_1, \tilde b_2) \]

  • under \(H_0\) \[(\tilde u_1, \tilde u_2, \tilde b_1, \tilde b_2) = {\arg\,\max}_{\Theta}\,\ell(u_2 + \Delta + (b_2-b_1)w_p, u_2, b_1, b_2)\]

  • under \(H_1\) \[(\hat u_1, \hat u_2, \hat b_2, \hat b_1) = {\arg\,\max}_{\Theta}\,\ell(u_1, u_2, b_1, b_2)\]

  • \(100(1-\alpha)%\) confidence interval for \((y_{1p}-y_{2p})\) can be obtained from the set of \(\Delta\) values that satisfy \(\Lambda(\Delta) \leq \chi^2_{(1), 1-\alpha}\)

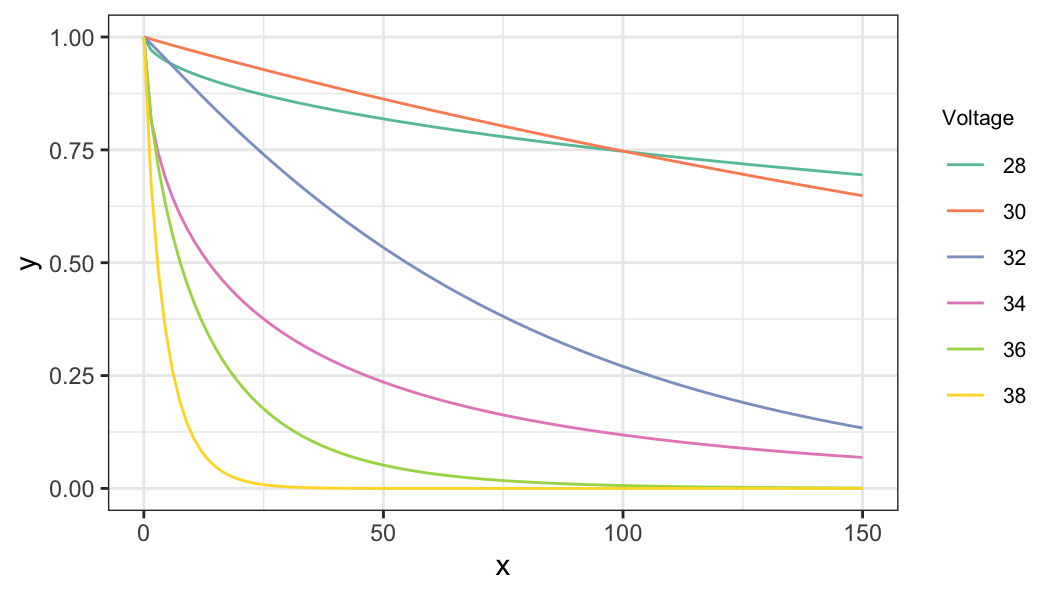
Comparison of Weibull or extreme value distributions

  • Assume \(T_{ji}\sim \text{Weibull}(\alpha_j, \beta_j)\) \((j=1, \ldots, m,\;\;i=1, \ldots, n_j)\)

    • Data \(\big\{(t_{ji}, \delta_{ji}), j=1, \ldots, m,\;\;i=1, \ldots, n_j\big\}\)

  • Survivor function of Weibull distribution \[ S_j(t) = \exp\big[-(t/\alpha_j)^{\beta_j}\big] \]

  • Survivor function of extreme value distribution \[ S_j(y) = \exp\big[-e^{(y-u_j)/b_j}\big] \]

    • \(u_j = \log \alpha_j\)

    • \(b_j = 1/\beta_j\)

Example 5.4.1

  • Data of the following table are on the time to breakdown of electrical insulating fluid subject to a constant voltage stress in a lifetest experiment

Estimate of voltage-specific extreme value models
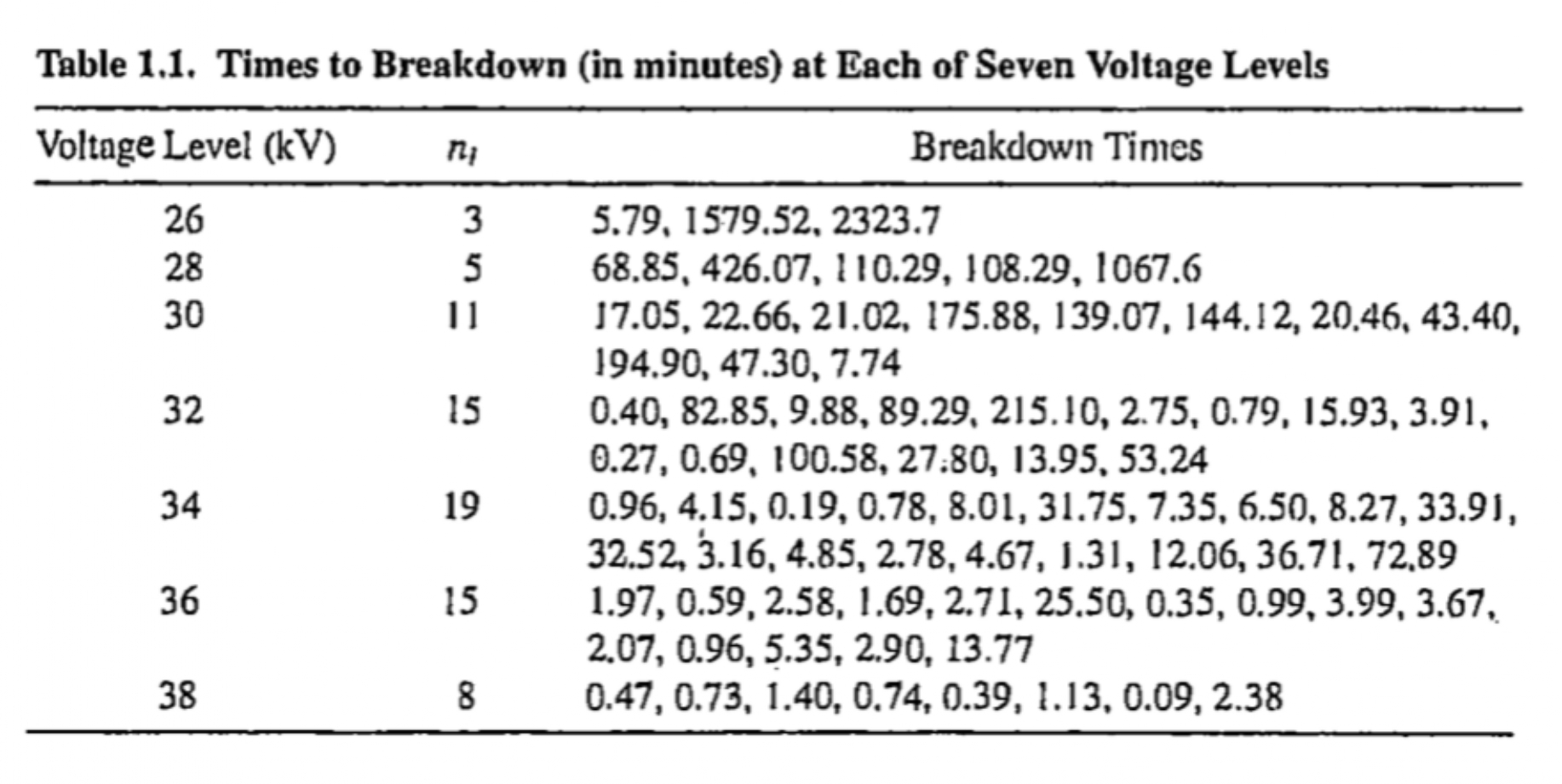
voltage \(\hat u_j \pm se(\hat u_j)\) \(\hat b_j \pm se(\hat b_j)\)
26 \(6.862 \pm 1.104\) \(1.834 \pm 0.885\)
28 \(5.865 \pm 0.486\) \(1.022 \pm 0.474\)
30 \(4.351 \pm 0.302\) \(0.944 \pm 0.303\)
32 \(3.256 \pm 0.486\) \(1.781 \pm 0.254\)
34 \(2.503 \pm 0.315\) \(1.297 \pm 0.211\)
36 \(1.457 \pm 0.309\) \(1.125 \pm 0.221\)
38 \(0.001 \pm 0.273\) \(0.734 \pm 0.367\)

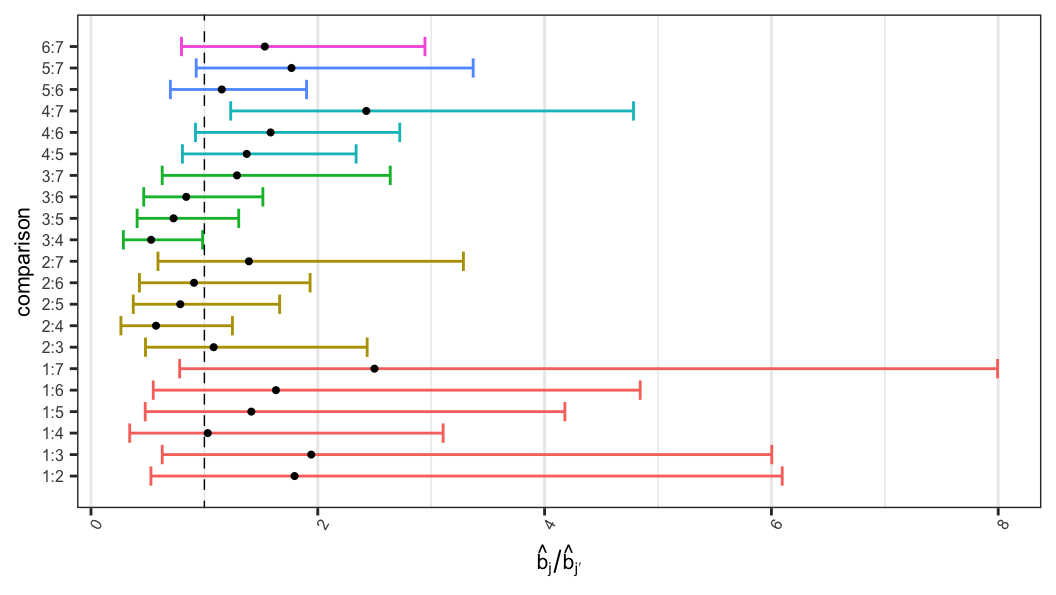
Comparison of estimated survivor function

LRT (Case 1)

  • Null hypothesis \[ H_0: b_1 = \cdots = b_7 \]

  • LRT statistic \[\begin{aligned} \Lambda & = 2\ell(\hat u_1, \ldots, \hat u_7, \hat b_1, \ldots, \hat b_7) - 2\ell(\tilde u_1, \ldots, \tilde u_7, \tilde b, \ldots, \tilde b) \\ & = 2(-132.181) - 2(-136.578) \\ & = 8.794 \end{aligned}\]

    • p-value \[ Pr(\chi^2_{(6)} \geq \Lambda) = 0.185 \] It does not provide enough evidence to reject the null hypothesis of equality of the scale parameters.

Confidence interval of \((b_1/b_2)\) (Case 2)

  • Wald-type \[\begin{aligned} (\log \hat b_1 - \log \hat b_2) &\pm z_{1-\alpha/2}\,se(\log \hat b_1 - \log \hat b_2) \\[.25em] (\hat b_1/\hat b_2)&\;e^{\pm z_{1-\alpha/2}\,se(\log \hat b_1 - \log \hat b_2)}\\[.25em] (1.834 / 1.022)&\;e^{\pm\,(1.96)(0.624)}\\[.25em] 0.529 & < (b_1/b_2) <6.095 \end{aligned}\]

    • Similarly confidence intervals for \((b_j/b_{j'})\) \(j>j'\) can be obtained

Estimate and 95% confidence interval of pair-wise comparisons of scale parameters \((b_j/b_{j'})\)

Case 3

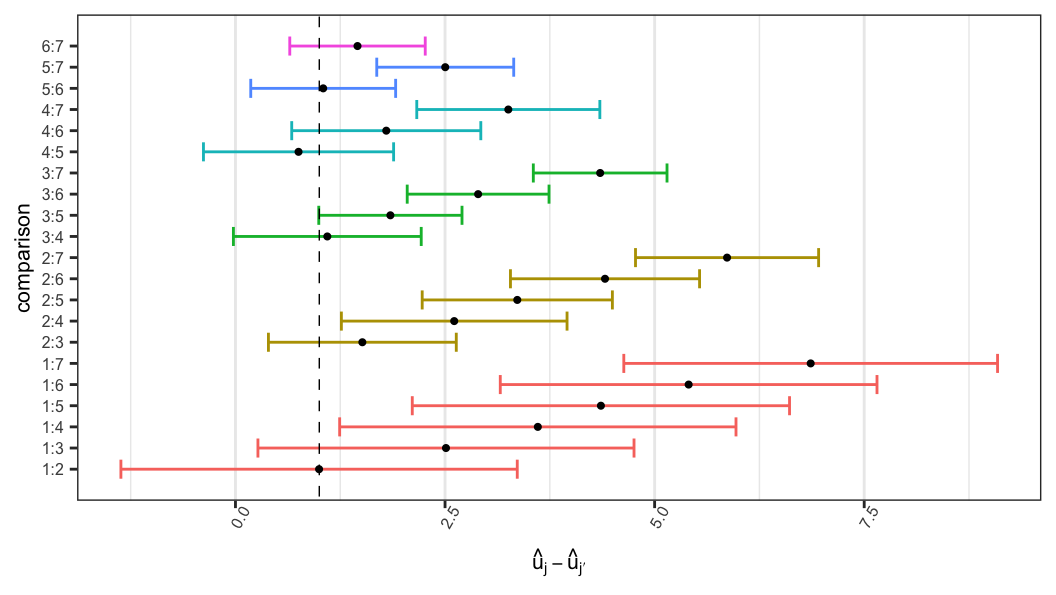
  • Equality of all location parameters when scales are equal \[ H_0: u_1 = \cdots = u_m, \; b_1=\cdots = b_m \]

  • LRT statistic \[\begin{aligned} \Lambda & = 2\ell(\tilde u_1, \ldots, \tilde u_m, \tilde b, \ldots, \tilde b)-2\ell(u^{\star}, \ldots, u^{\star}, b^{\star}, \ldots, b^{\star})\\[.25em] &= 2(-136.578) - 2(-176.584) \\[.25em] &= 80.013 \end{aligned}\]

    • p-value \(P\big(\chi^2_{(1)} > 80.013\big) < .001\;{\color{purple}\rightarrow}\) There is a strong evidence against the assumption of equality of \(m\) location parameters

Case 4

  • Wald-type confidence interval of \((u_1-u_2)\) \[\begin{aligned} (\hat u_1 - \hat u_2) &\pm z_{1-\alpha/2}\;se(\hat u_1 - \hat u_2) \\[.25em] (6.862 - 4.351) &\pm (1.96)(1.206) \\[.25em] -1.367 &<(u_1 - u_2) < 3.361 \end{aligned}\]

    • There is no significant difference between \(u_1\) and \(u_2\)

Estimate and 95% confidence interval of pair-wise comparisons of location parameters \((u_j - u_{j'})\)

Case 5

  • General expression of \(p\)th quantile of the group \(j\) \[ y_{jp} = u_j + b_j w_p, \;j=1, \ldots, m \]

  • Difference of \(p\)th quantile between groups 1 and 2 \[ y_{1p} - y_{2p} = u_1 - u_2 + (b_1 - b_2)w_p \]

    • 95% confidence interval for the difference of median between groups 1 and 2 \[\begin{aligned} \hat{y}_{1m} - \hat{y}_{2m} &\pm z_{1-\alpha/2} se(\hat{y}_{1m} - \hat{y}_{2m}) \\[.25em] (6.19 -5.491)& \pm (1.96)(1.291) \\[.25em] -1.831 & <(y_{1m}-y_{2m}) <3.231 \end{aligned}\]

Estimate and 95% confidence interval of pair-wise comparisons of medians \((y_{j, .5} - y_{j', .5})\)

Homework

  • Analyse the breakdown time data using log-logistic and log-normal distributions and compare the results with that of Weibull distribution