| time | status |
|---|---|
| 2 | 1 |
| 72 | 0 |
| 51 | 1 |
| 60 | 0 |
| 33 | 1 |
| 27 | 1 |
| 14 | 1 |
| 24 | 1 |
| 4 | 1 |
| 21 | 0 |
Chapter 4
(AST405) Lifetime data analysis
4 Inference procedures for parametric models
Introduction
-
Likelihood methods for lifetime data were introduced in Chapter 2, which includes derivation of likelihood function for different types of censored data
Maximum likelihood estimator
Inference about parameters (hypothesis testing and confidence intervals)
Likelihood function (Complete data)
Let
Likelihood and log-likelihood function
Maximum likelihood estimator (MLE)
Statistical inference (Complete data)
-
Large sample property of MLE
Fisher expected information matrix
Observed information matrix
Likelihood function (Type I or random censoring)
-
Data:
lifetime
censoring time
Data for type I or random censoring
Likelihood function
Likelihood function (Type II censoring)
Let lifetime
The experiment was terminated after observing
The remaining
Likelihood function
Statistical inference (censored sample)
For censored samples, the result “asymptotic distribution of MLE is normal” is still valid
The expression of the Fisher expected information matrix
4.1 Exponential distribution
The exponential distribution is the first lifetime model for which statistical methodology were extensively developed
Exact tests can be developed for exponential distribution for certain type of censoring mechanism
Exponential distribution assume constant hazard and its use is limited for analyzing real life problems
Probability density function
Hazard function
Survivor function
Homework
- Estimation and related inference of exponential distribution when the sample has no censored observations
Type I or random censoring
Lifetime
Data:
Likelihood function
Likelihood function
-
Log-likelihood function
-
-
Log-likelihood function
-
MLE
- Assuming
- Assuming
- Information matrix
- Replacing the parameter
Confidence interval (Method I)
Using
For a small sample,
For a sample with a small number of uncensored observations,
Confidence interval (Method II)
-
Sprott (1980) showed that
MLE
Observed information matrix
-
Pivotal quantity
- Approximation of
- Approximation of
Confidence interval (Method III)
- Likelihood ratio statistic
LRT statistic
Two-sided
Confidence interval of survivor function
Confidence interval for the parameter
Let
-
Confidence interval of hazard function
-
Example 4.1.1
- Lifetimes (in days) of 10 pieces of equipment
- Assume lifetimes follow exponential distribution with parameter, i.e.
MLE
95% confidence interval of
-
95% confidence interval of
Confidence interval for
Confidence interval for
-
Likelihood ratio statistic
95% CI for
95% CI for
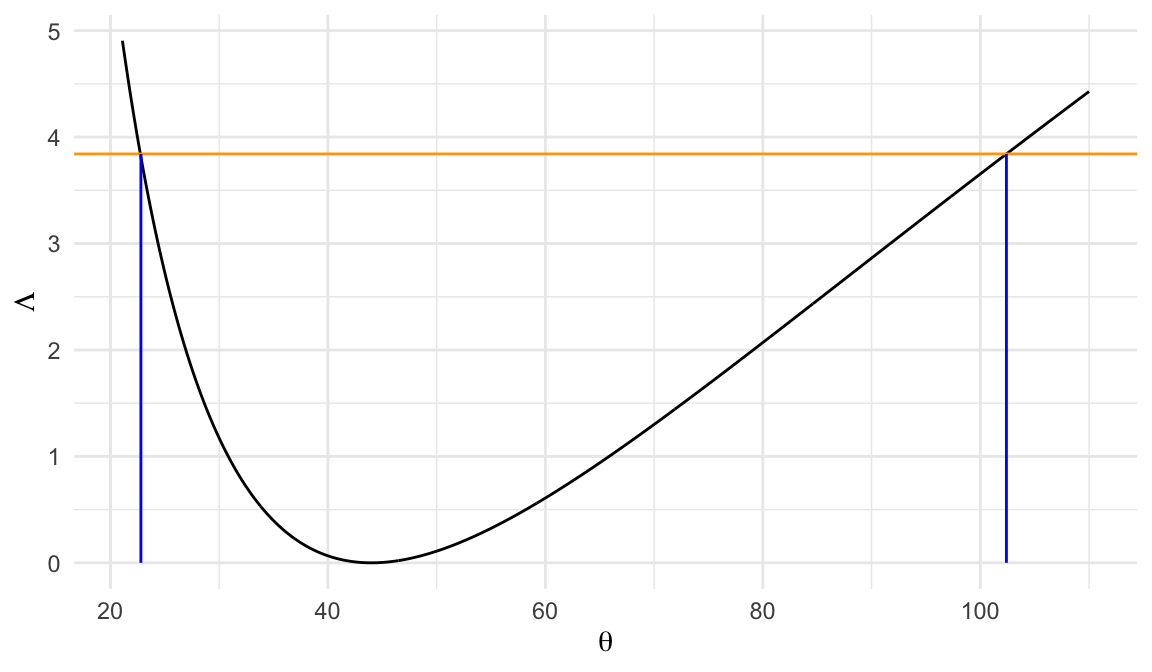
| method | lower | upper |
|---|---|---|
| Normal approx. | 11.40 | 76.60 |
| Sprott | 22.69 | 103.03 |
| LRT | 22.80 | 102.40 |
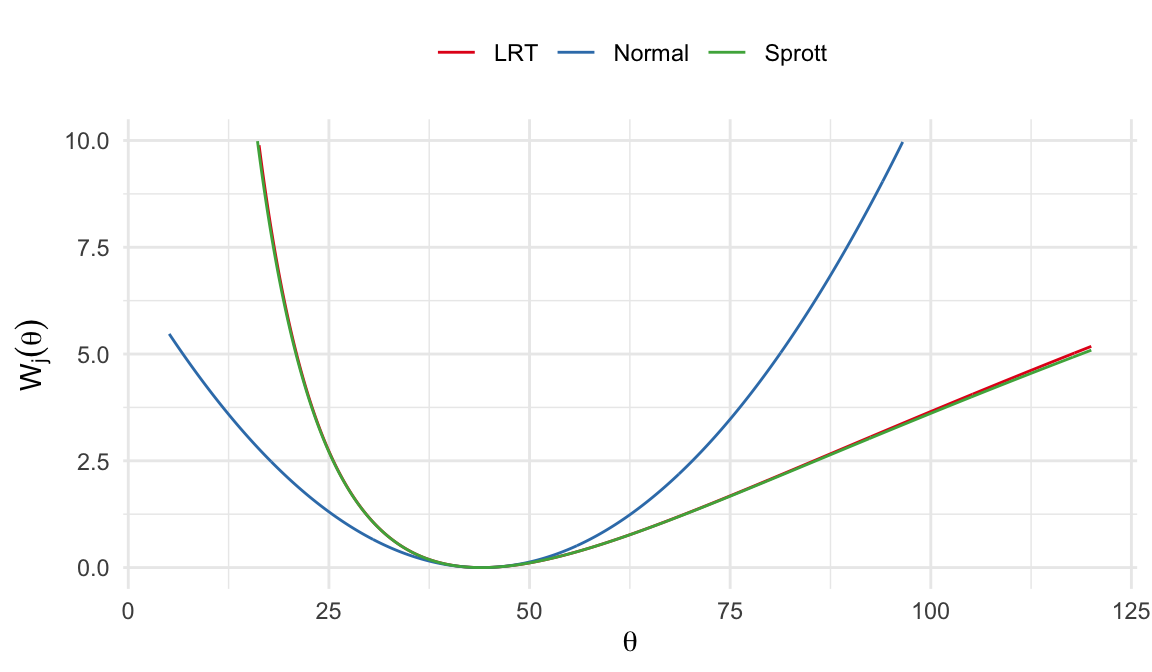
Methods for CI
Normal approximation
Sprott’s method
LRT
Type II censoring plan
Assume lifetime
Let
The joint distribution of
- The log-likelihood function
-
Maximum likelihood estimator
- Observed information matrix
- Observed information matrix
Exact confidence interval
Exact confidence interval for
In general
- It can be shown that
- The joint distribution of
- We can write
-
The joint distribution of
- Using Equation 4.1
-
Equation
-
-
Since
Then using the relationship between gamma and chi-square distribution
Review
- Moment generating functions for different distributions
-
Since
-
-
Example 4.1.3
The first 8 observations in a random sample of 12 lifetimes (in hours) from an assumed exponential distribution are
-
Homework
- Obtain 95% exact and approximate confidence intervals for
- Obtain 95% exact and approximate confidence intervals for
4.1.3 Comparison of distributions
Comparison of two or more lifetime distributions is often of interest in practice
For comparing two or more independent exponential distributions, different methods of hypothesis tests and confidence intervals are available
Likelihood ratio tests
Let
Assume
Data:
The likelihood function for
The corresponding log-likelihood function
- The log-likelihood function
-
-
- Maximum likelihood estimator of
-
Under
- Under
- Under
-
Likelihood ratio test statistic
- Under
- Under
Example 4.1.4
Four independent samples of size 10 each had 7 failures
MLE under exponential model
-
Homework
- Test
- Test
Confidence intervals for
Comparison between two exponential distributions
It can be shown that mle
Distribution of
Null hypothesis
Test statistic
95% CI for
95% CI for
Confidence intervals can also be found by inverting the likelihood ratio test for a hypothesis of the form
-
For Type I sample
- MLE
- MLE
-
Under
- MLE under
- MLE under
- The likelihood ratio test statistic
and
- The likelihood ratio test statistic
For Type I censored sample, LRT statistics based confidence interval for
Example 4.1.5
A small clinical trial was conducted to compare the duration of remission achieved by two drugs used in the treatment of leukemia.
Duration of remission is assumed to follow an exponential distribution and two groups of 20 patients produced the followings under a Type I censoring mechanism
Obtain 95% approximate and exact CI for
Unrestricted MLEs
95% approximate CI for
- 95% approximate CI (normal distribution based) for
Is there any significant difference between
Likelihood ratio statistic based confidence interval for
Estimates under
Likelihood ratio statistic
| 0.525 | 3.953 | 3.185 | 3.911 |
| 0.560 | 3.424 | 3.150 | 3.819 |
| 0.595 | 2.958 | 3.115 | 3.726 |
| 0.630 | 2.549 | 3.080 | 3.633 |
| 0.665 | 2.187 | 3.045 | 3.541 |
| 0.700 | 1.869 | 3.010 | 3.448 |
| 0.735 | 1.589 | 2.975 | 3.356 |
| 0.770 | 1.341 | 2.940 | 3.263 |
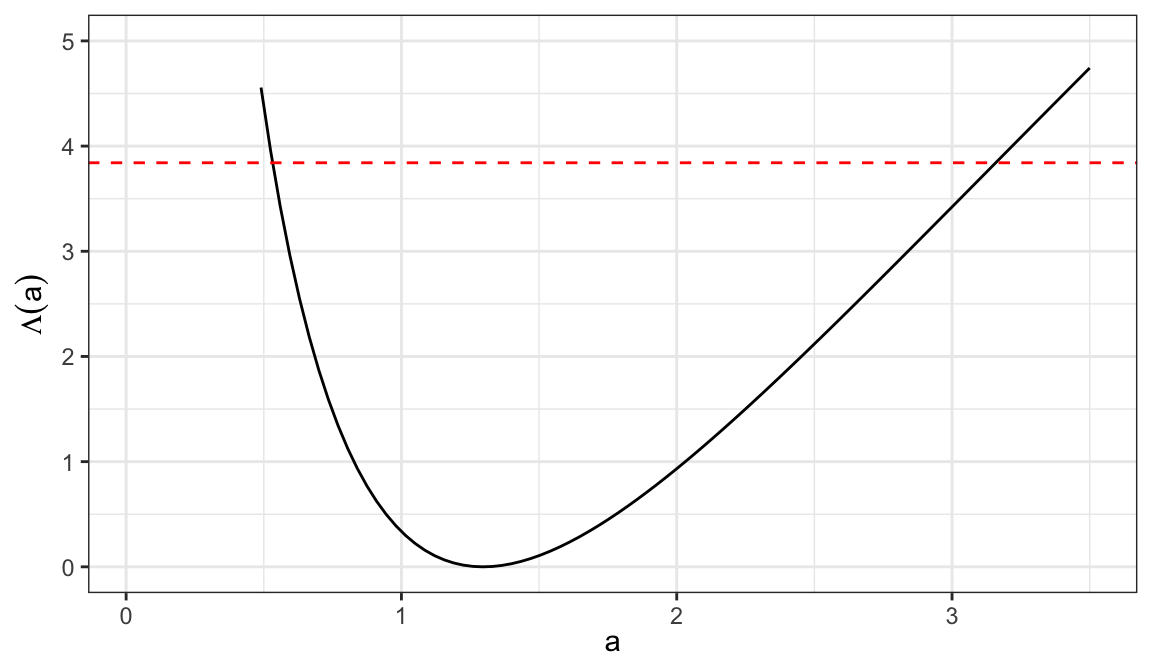
- 95% of
| method | lower | upper |
|---|---|---|
| Normal approximation | 0.54 | 3.114 |
| LRT | 0.56 | 3.150 |
Type II censored sample (CI for
Lifetime distributions
Type II censored sample for the group
- Likelihood function
MLE
We have already shown that
Then we can show
We can write
4.2 Gamma distribution
-
The pdf of two-parameter gamma distribution
- Scale parameter
- Scale parameter
Survivor function
Incomplete gamma function
Uncensored data
-
Let
-
-
- Score functions
-
MLE
Two equations and two unknowns
Equations are non-linear in terms of the variables
No closed form solutions
1. Substitution method
Solve Equation 4.5 using a suitable optimization technique (e.g. graphical method, Newton-Raphson method, etc.) to obtain
Then
2. Newton-Raphson method
- Score functions
- Elements of Hessian matrix
Score vector
Hessian matrix
Score vector and information matrix are function of parameters and data
Initial values
Updated estimate
The estimate
Repeating the procedure of evaluating the Equation 4.6 using the current estimate, the following sequence of estimates can be obtained
- A convergence criterion needs to be defined to obtain the MLE from the sequence of estimates
Convergence criteria are defined on the basis of two successive values of the parameters estimates
-
- Estimated variance-variance matrix of the MLE
Newton-Raphson method: Pseudo code
1: theta0 <- `initial value of the parameter`
2: eps <- 1
3: while (eps > 1e-5) {
4: u0 <- U(theta0)
5: h0 <- H(theta0)
6: theat1 <- theta0 - inv(h0) * u0
7: eps <- max(abs(theta1 - theta0))
8: if (eps < 1e-5) break
9: else theta0 <- theta1
10: }
11: return (list(theta0, h0))-
Statistical software have routines (such as
optim()of R) that can optimize likelihood function to obtain MLESuch routines require providing a “function” of likelihood function as an argument
Different optimization algorithms, such as Newton-Raphson, Mead-Nelder, simulated annealing, etc. are implemented in optimization routines
Statistical inference
Asymptotic distributions of MLEs, i.e.
-
Since
-
-
Example 4.2.1
Following are survival time of 20 male rates that were exposed to a high level of radiation
rtime <- c(152, 152, 115, 109, 137, 88, 94, 77, 160, 165, 125, 40, 128, 123, 136, 101, 62, 153, 83, 69)
rtime [1] 152 152 115 109 137 88 94 77 160 165 125 40 128 123 136 101 62 153 83
[20] 69- Assume the lifetimes follow a gamma distribution with scale parameter
From the data:
Expressions of the score function
- R function
uniroot()can be used to obtain the value of
Log-likelihood function of gamma distribution
- R function to calculate log-likelihood function of a gamma distribution for a given sample
paris a vector with the parameterscaleas the first element andshapeas the second elementtimeis the observed failure timesgamma_loglkfunction can be evaluated for any given valid values ofparandtime
- For given values of parameters, say
gamma_loglk(par = c(1, 2), time = rtime)[1] -2175.531- For another set of values
gamma_loglk(par = c(100, 80), time = rtime)[1] -5392.711
optim() function
- R function
optim()is a general purpose optimization routine
parfngrmethodloweranduppercontrolfnscale, etc.) for controlling the iterations
Initial values
Initial values of the parameters can be selected from the exploratory plots of log-likelihood function
The log-likelihood function must provide finite values with the initial values of the parameters
- As an example, assume the initial values
gamma_loglk(par = c(12.9, 8.8), time = rtime)[1] -100.48- For another set of initial values,
gamma_loglk(par = c(1.0, 1.0), time = rtime)[1] -2269- Since both sets of initial values can provide finite values of log-likelihood function, we can use either of these two as an initial value for optimizing the log-likelihood function using the R function
optim()
Example 4.2.1 using optim()
- Fit of the gamma distribution to the rat data
- List of objects in
gamma_fit
names(gamma_fit)[1] "par" "value" "counts" "convergence" "message"
[6] "hessian" - Converged?
gamma_fit$convergence[1] 0- Estimate of scale and shape parameters
gamma_fit$par[1] 12.896976 8.795312-
- Estimated variance-variance matrix
cvar <- solve(-gamma_fit$hessian)
cvar [,1] [,2]
[1,] 16.88167 -10.871356
[2,] -10.87136 7.416138
Using the sampling distribution of
Using the sampling distribution of
Quantiles
-
-
qgamma(p, scale=1, shape)]
-
Estimate of the median for the rat data is
12.893951 * qgamma(.5, scale = 1, shape = 8.799089) [1] 109.1872qgamma(.5, scale = 12.893951, shape = 8.799089)[1] 109.1872Likelihood ratio statistic
Likelihood ratio statistic
Approximate
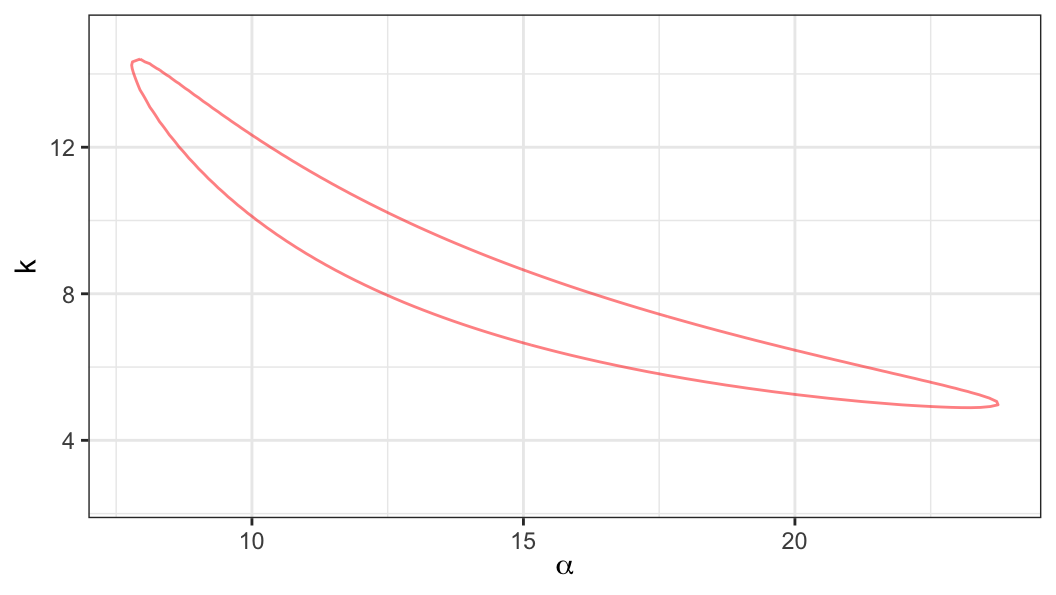
LRT statistic based CI for
Consider the following null hypothesis
MLEs (unrestricted and under restriction)
-
Likelihood ratio statistic
- Under
- Under
An approximate two-sided
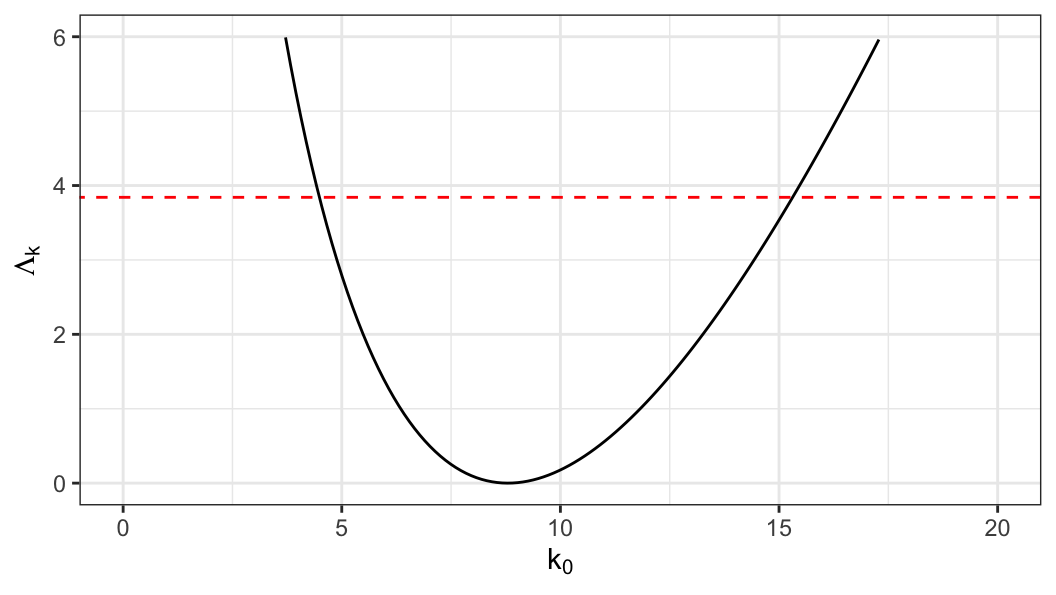
LRT statistic based CI for
Consider the following null hypothesis
MLEs (unrestricted and under restriction)
-
Likelihood ratio statistic
- Under
- Under
An approximate two-sided
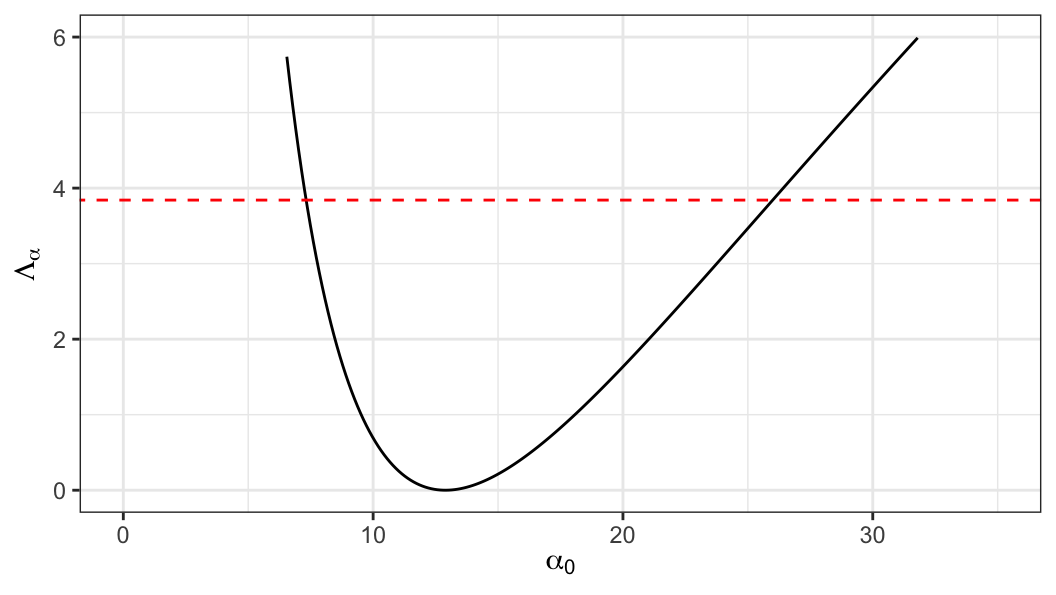
Summary of
For
For
Censored
Data
No closed form solutions are available for MLEs
Algebraic expressions of score function and information matrix for the log-likelihood function
Score functions and information matrix can be evaluated numerically
-
Optimization routines available in statistical software can be used to obtain MLEs
- Different optimization algorithms such as Newton-Raphson, Nelder-Mead, etc. are available in such routines
As an example, we are going to use the same rat data that we have used for the analysis of complete data
-
For the rat data, assume a time
- An R object
rtimecis created, which has two columnstimeandstatus
- An R object
rtimec |> t() [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
time 152 152 115 109 137 88 94 77 160 165 125 40 128
status 0 0 1 1 1 1 1 1 0 0 1 1 1
[,14] [,15] [,16] [,17] [,18] [,19] [,20]
time 123 136 101 62 153 83 69
status 1 1 1 1 0 1 1gamma log-likelihood function for censored sample
gamma_loglk <- function(par, time, status = NULL) {
#
if (is.null(status)) status <- rep(1, length(time))
#
llk_f <- sum(status * dgamma(time, scale = par[1],
shape = par[2], log = T))
#
llk_c <- sum((1 - status) * pgamma(time, scale = par[1],
shape = par[2], lower.tail = F,
log.p = T))
return(llk_f + llk_c)
}Censored sample
- R codes to obtain MLE of parameters of a gamma distribution from a censored sample
Maximum likelihood estimators [
gamma_out_c$par]Standard errors [
solve(-gamma_out_c$hessian)]
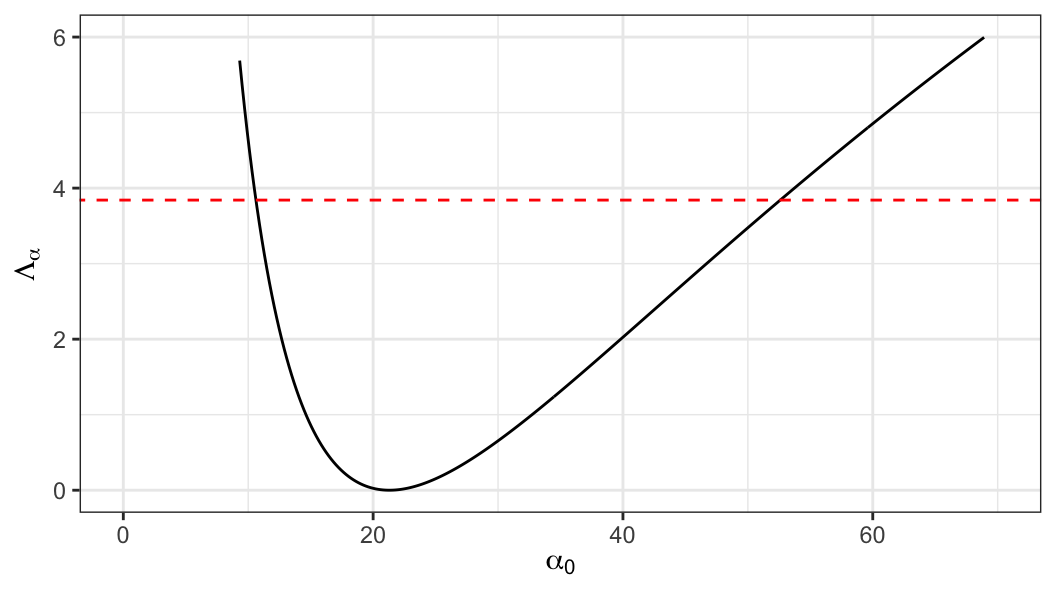
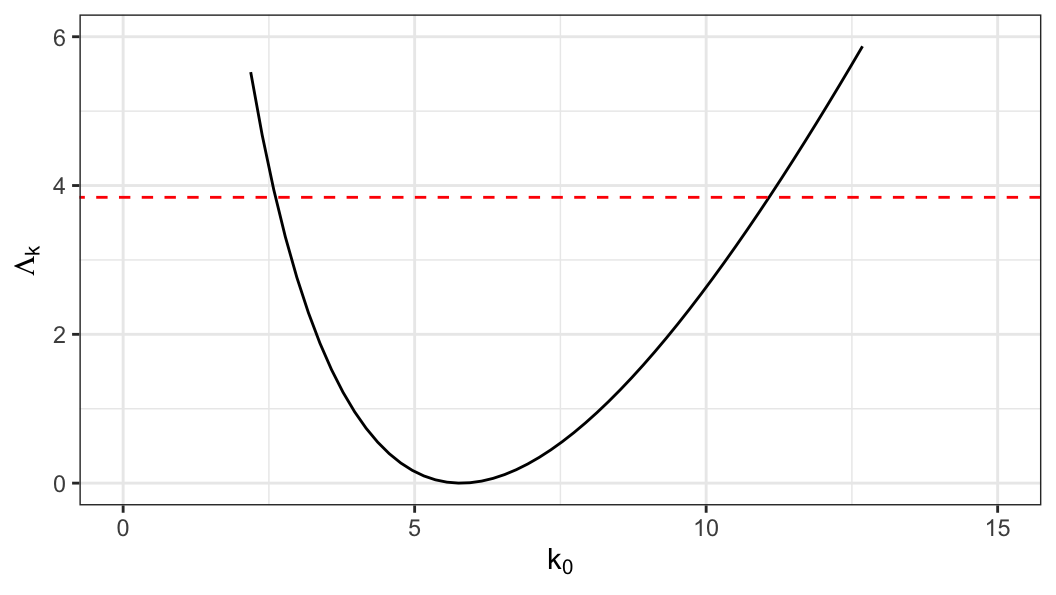
- Estimate of median
Acknowledgements
This lecture is adapted from materials created by Mahbub Latif