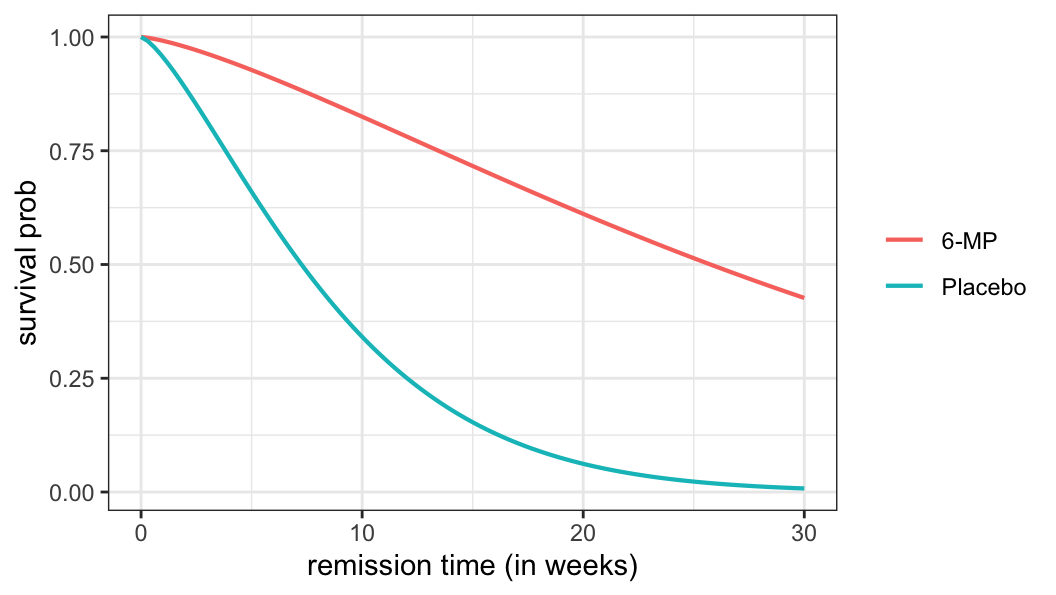
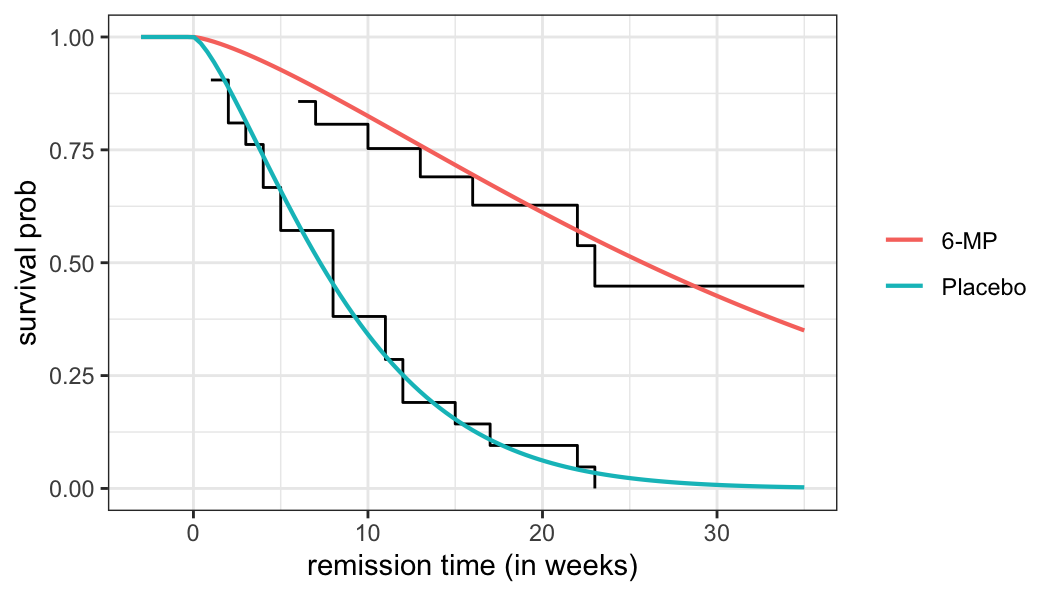
glimpse(gehan65)Rows: 42
Columns: 3
$ time <dbl> 6, 6, 6, 6, 7, 9, 10, 10, 11, 13, 16, 17, 19, 20, 22, 23, 25, 3…
$ status <dbl> 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
$ drug <chr> "6-MP", "6-MP", "6-MP", "6-MP", "6-MP", "6-MP", "6-MP", "6-MP",…